¿Sabías que puedes aumentar la precisión (pero no la exactitud) del sensor LM35?
El sensor de temperatura LM35 entrega 10mV por cada grado centígrado. A 25 grados reporta 250 mV, mientras que a 150 grados reporta 1500 mV. ¿Esto es bueno o malo? Es malo si estás considerando utilizar un convertidor analógico-digital (ADC) de 10 bits como el encontrado en muchos microcontroladores (como el ATmega328 del Arduino UNO).
Por ejemplo, uno de estos convertidores entregaría el valor digital 51 a una temperatura de 25 grados, mientras que a 26 grados entregaría el valor digital 53. ¡En un grado centígrado solamente existen dos pasos!
¿Podemos lograr tener más pasos por grado centígrado? Claro que sí, y sigue leyendo para que te enteres cómo lo puedes lograr, sus pros y sus contras.
¿Porqué aumentar la precisión?
¿Qué implica tener dos pasos por grado centígrado? Pues que la resolución máxima del sistema serían 0.5 grados: 25.0, 25.5, 26.0, 26.5, … . Para muchas aplicaciones tener medio grado centígrado de precisión es suficiente, pero para otras no lo es. Si estás construyendo un controlador PID necesitas más precisión, por ejemplo, 10 o más pasos por grado centígrado: 25.0, 25.1, 25.2, … .
¿Qué necesitas para aumentar la precisión del LM35? Nada más dos cosas: un amplificador operacional en modo No Inversor, y (un poco de) álgebra básica.
Precisión y exactitud no son lo mismo. Aunque muchas veces ambos términos son utilizados de manera indistinta, significan cosas diferentes relacionadas al mismo fenómeno. Con lo que te voy a explicar a continuación podrás aumentar la precisión del sensor hasta un cierto límite físico, pero la exactitud del mismo (0.5 grados) es parte inherente de él y no hay mucho que puedas hacer para mejorarla.
Vamos a aclarar algunos conceptos para que estemos en el mismo canal en esta conversación:
Exactitud
Exactitud significa qué tan cerca está el valor medido del valor real. Entre más cerca, más exacto.
La exactitud del LM35 es de más-menos 0.5 grados centígrados. En el peor de los casos el LM35 reportaría un valor 0.5 grados alejado (hacia arriba o hacia abajo) del valor real de temperatura, y no hay nada que puedas hacer para cambiar este comportamiento ya que es inherente al sensor.
Precisión
Precisión significa qué tan cercanos están unos de otros los valores reportados por el instrumento de medición.
Como mencioné, si tomas la lectura directa del LM35 solamente tendrás dos pasos por cada grado centígrado. Pero aquí, a diferencia de la exactitud y dentro de algunos límites, podrás aumentar la precisión del mismo, por ejemplo, tener 10 (o más) pasos por grado centígrado.
En este punto llegamos a algunas combinaciones que volvían locos a mis alumnos de la materia Programación Avanzada y Métodos Numéricos:
- Puedes tener un instrumento muy exacto, pero poco preciso.
- Puedes tener un instrumento muy preciso, pero poco exacto.
Precisión del convertidor ADC
El convertidor ADC de tu microcontrolador también tiene sus propios parámetros de exactitud y precisión. El que nos interesa es el segundo, ¿a cuántos volts equivale cada paso (lectura) del convertidor? Esta pregunta se responde a partir del número de bits del convertidor y la tensión de trabajo del mismo. A mayor número de bits mayor será su precisión.
Como ejemplo toma el ATmega328, el cual tiene un convertidor de 10 bits (2^10 = 1024 pasos) y 5 volts de tensión de trabajo. Por lo tanto, cada paso (lectura) del convertidor equivale a 4.88 mV (4.88mV = 5V / 1024).
Aquí viene lo interesante: el LM35 entrega 10mV por grado centígrado, y el ADC entrega un paso cada 4.88mV, ¡solamente hay 2 pasos por grado centígrado!
¿Cómo puedes aumentar el número de pasos por grado centígrado, es decir, cómo puedes mejorar la precisión del sensor? Muy fácil, con un amplificador operacional en modo No Inversor, álgebra y programación.
Álgebra
Supón que ya tienes al amplificador (hablaremos de él más adelante) y lo configuraste para tener una ganacia de 11. Con esto lograrás tener 110mV por grado centígrado (110mV/C = 10mV/C x 11). De esta manera ahora tendrás 22 pasos por grado centígrado (22 = 110mV/C / 4.88mV). ¡Haz logrado pasar de una precisión de 0.5 grados a una de 0.045!
¡Wow! ¿Y porqué limitarte a una ganancia de 11 cuando puedes tener una de 100 o de 1000? ¡Pues porque hay límites físicos! El aumento en la precisión implica que tienes que reducir el rango de medición. Esto es, cada vez que aumentas la precisión el rango de temperatura a medir se reduce. Con la ganancia de 11 la temperatura máxima que se puede medir (sin pasarse de 5V) es de 47.5 grados centígrados. Nada es gratis en la vida.
Y aunque sería grandioso escoger valores de ganancia arbitrarios enormes, no se puede. La tensión de trabajo del ADC es de 5V y cualquier tensión por arriba puede dañar al módulo o al chip. Imagina que tienes una ganancia de 100, lo cual equivale a 204 pasos por grado centígrado (204 = (10mV/C)x(100) / (4.88mV/C)). ¿Cuál es la temperatura máxima que podrás medir? R: 5 grados. Esto es, tu rango de temperatura medible, sin pasarte de 5V, es de sólo 5 grados:
- Si G=100, (10mV/C)x(100) = 1000mV/C.
- (1000mV/C) / (4.88mV) = 204 pasos por grado centígrado.
- (1024 pasos) / (204 pasos/C) = 5 grados centígrados.
Por lo visto no es buena idea escoger una ganancia tan grande y de forma tan arbitraria, ¿cierto? En la siguiente sección calcularás la ganancia máxima para una temperatura máxima dada.
Ejercicio: Haz los cálculos que demuestren que la ganancia máxima que contemple el rango completo del LM35 (150 grados) es 3.33.
Cálculos prácticos
Para determinar la ganancia máxima para una temperatura máxima aplica los siguientes pasos:
- Escoge la temperatura máxima que deseas medir. Por ejemplo, T = 50 grados centígrados. Esto significa que cuando el ADC reporte el valor 1023 (el máximo), entonces tendrás 50 grados.
- Calcula cuántos pasos habrá por cada grado: p = (1024 pasos) / (50 grados) = 20.48 pasos por grado centígrado.
- Calcula a qué tensión corresponde el resultado anterior, v = ( 20.48 pasos/C) x (4.88mV/paso) = 99.94mV por grado centígrado.
- Calcula la ganancia máxima para tu valor de temperatura, G = (99.94mV/C) / (10mV/C) = 9.99.
Por lo tanto, la ganancia G máxima para una temperatura máxima de 50 grados centígrados es de 9.99. Cualquier valor de temperatura por arriba de 50 entregará tensiones por encima de 5V, lo cual podría dañar al módulo ADC o al chip.
Amplificador
¿Y cómo implementas la ganancia recién calculada? Pues a través de un circuito amplificador. Éste lo puedes construir con diversas tecnologías, pero lo más simple y efectivo es que utilices un amplificador operacional (opamp) configurado como amplificador no inversor. Para este ejemplo usaremos un LM358, el cual integra dos opamps en un encapsulado de 8 terminales, pero cualquier otro funciona.
A partir de la ecuación del amplificador no inversor, G = 1 + R2/R1, debes escoger una R y calcular la otra. Por ejemplo, si escoges que R2 sea de 100K (100 Kilo Ohmios), entonces tienes que despejar R1 de la ecuación anterior, la cual te queda: R1 = R2 / (G-1), y substituyendo los valores conocidos del ejemplo anterior tenemos que R1 = (100K) / (9.99-1) = 11.12K, cuyo valor comercial más cercano es 11K.
El diagrama eléctrico para una ganancia de 11 es el siguiente:
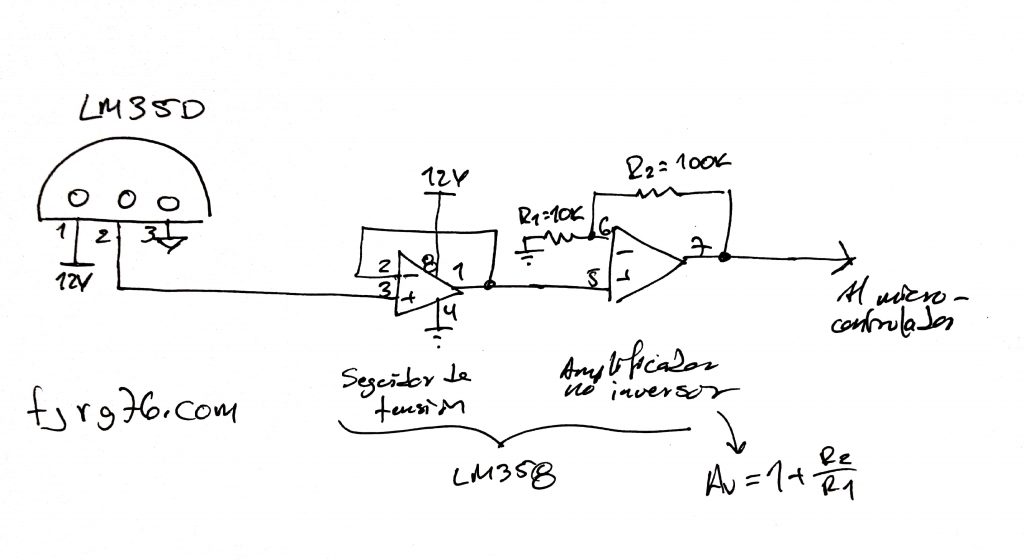
Ejercicio: Calcula la temperatura máxima que puedes medir a partir del valor de R1 recién encontrado (11 Kilo Ohmios), es decir, ajusta los cálculos a partir de los valores reales.
Programación
El último paso es escribir un programa que lea la temperatura analógica del LM35 y haga algo con ella, por ejemplo, imprimirla (en el puerto serial o en un LCD). Para esto vas a necesitar el valor de la temperatura máxima (teórica o ajustada según los valores de resistencias comerciales). Siguiendo con el ejemplo: T = (50 grados x lectura_del_ADC) / (1024 pasos) y el resultado queda en grados centígrados:
float temperature = ( 50.0 / 1024 ) * analogRead( A0 );
Ejemplo
El siguiente código (para Arduino en formato de sketch) utiliza los siguientes valores: R1=10K, R2=100K, G=11, Tmax=45.45 grados centígrados. Agregué un filtrado de datos, pero eso no te debe distraer del objetivo del ejemplo:
void setup()
{
pinMode( 13, OUTPUT );
Serial.begin( 115200 );
}
void loop()
{
uint16_t rawReading = 0;
for( uint8_t i = 8; i > 0; --i ){
rawReading += analogRead( A0 );
}
float temp_in_centi = ( 45.45 / 1024.0 ) * ( rawReading >> 3 );
Serial.println( temp_in_centi, 3 );
delay( 500 );
}
La instrucción
rawReading >> 3
toma el acumulado rawReading y lo divide entre 8 (el número de lecturas). Una expresión equivalente es: rawReading / 8.
Resultados
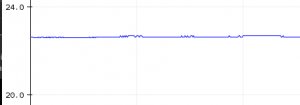
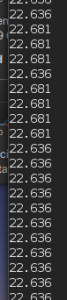
El programa anterior arroja los siguientes resultados, tanto en formato numérico como en gráfica.
La curva es muy plana, o dicho de otra forma, los valores son muy estables debido a 3 cosas: la temperatura ambiente fue constante, la precisión que hemos añadido con la técnica explicada, y el filtro promediador de 8 muestras. En la tabla puedes observar dos valores separados por un paso: 22.681 y 22.636. Si calculas la diferencia entre ellos obtendrás 0.045 grados centígrados por paso, lo cual es consistente con los cálculos para este ejemplo: 0.045=1 / (22.52 pasos por grado centígrado).
Resumen
En este artículo viste la manera de aumentar la precisión del sensor de temperatura LM35 amplificando su señal, las diferencias entre exactitud y precisión, y que nada en la vida es gratis: si aumentas la precisión disminuyes la temperatura máxima a medir.
¿Qué sigue?
¿Y qué si deseamos reducir el rango, por ejemplo de 30 a 40 grados centígrados? La lectura 0 del ADC correspondería a 30, mientras que la lectura 1023 correspondería a 40.
Así mismo, en este artículo consideré la versión LM35DZ, la cual tiene un rango de 0 a 150 grados centígrados. Las otras versiones del mismo manejan rangos diferentes. Un trabajo futuro consistiría en modificar el circuito eléctrico para que incluya un desplazador de tensión. Del ejemplo del párrafo anterior deberíamos de alguna manera restarle 300 mV a la señal del LM35 para que con ello comencemos a contar a partir de 30 grados centígrados. Pero esto es tema de un siguiente artículo.
¡Suscríbete si esta entrada te gustó o si aprendiste algo nuevo!
Mi perfil completo lo puede encontrar en: https://www.linkedin.com/in/fjrg76-dot-com/
- Is your code asking too many questions? Learn how the “Tell, Don’t Ask” principle can make your objects do the talking - enero 6, 2024
- A Beginner’s Step-by-step Guide to Custom Power Symbols in KiCAD - enero 6, 2024
- ¡Hazlo, no preguntes! O sobre cómo dejar de abusar de los getters - diciembre 9, 2023
3 COMENTARIOS